2.2 仿真结果分析
图2、图3、图4为铝合金圆筒壳体在外径80mm和筒的长度110mm不变的情况下,圆筒内径分别为78mm、76mm、74mm不同壁厚的1阶模态变形图。从这些图上可以得到第一阶屈曲载荷因子(包括在顶面施加轴向载荷以及在圆筒壳体外壁施加载荷)并如表2所示。图5、图6为铝合金圆筒壳体在外径80mm和内径98mm不变的情况下,圆筒长度分别为106mm、102mm不同长度的1阶模态变形图,同时结合图1可以得到不同长度下的第一阶屈曲载荷因子(包括在顶面施加轴向载荷以及在圆筒壳体外壁施加载荷)并如表3所示。由于施加载荷均为1MPa,根据得到的第一阶屈曲载荷因子,可知每个模型的屈曲压力值为该模型的第一阶屈曲载荷因子与施加载荷(1MPa)的乘积。故第一阶屈曲载荷是屈曲载荷的最低值即为第一阶临界载荷,因此这意味着在理论上,当压力达到第一阶临界载荷时结构将失稳。
根据表2、表3可以得到不同壁厚的圆筒壳体、不同圆筒长度的壳体与临界载荷的关系,如图7、图8所示。
表2 不同壁厚下模型的第一阶屈曲载荷因子和临界载荷
表3 不同长度下模型的第一阶屈曲载荷因子和临界载荷
图7 铝合金壳体壁厚与临界载荷的关系(左:顶面轴向右:壳体外壁)
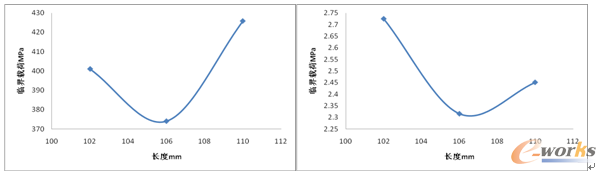
图8 铝合金壳体长度与临界载荷的关系(左:顶面轴向右:壳体外壁)
图7可以看出,随着壁厚的增大,铝合金圆筒壳体的临界载荷也随着增大并呈非线性关系。由于壁厚的增加,壳体失稳需要的载荷也随着增加。从图8可以看出,随着壳体长度的减少,临界载荷先减小再增大,在106mm附近存在一个长度值,使得临界载荷最小,可以根据仿真分析选取适合的长度。
3 结论
利用ANSYS对铝合金圆筒壳体外径80mm和筒的长度110mm不变,圆筒内径分别为78mm、76mm、74mm不同壁厚的情况下以及外径80mm和内径98mm不变,圆筒长度分别为106mm、102mm的情况下的壳体失稳状态进行仿真分析,得出结论如下:
(1)利用ANSYS屈曲分析可以得到第一阶屈曲载荷因子,由于施加载荷为1MPa,可知每个模型的屈曲压力值为该模型的第一阶屈曲载荷因子与施加载荷(1MPa)的乘积。故第一阶屈曲载荷是屈曲载荷的最低值即为第一阶临界载荷,因此这意味着在理论上,当压力达到第一阶临界载荷时结构将失稳
(2)在一定的壁厚范围内,随着壁厚的增大,铝合金圆筒壳体的临界载荷也随着增大并呈非线性关系。
(3)在一定的长度范围内,随着壳体长度的减少,临界载荷先减小再增大,并且存在一个长度值,使得临界载荷最小,可以根据仿真分析选取适合的长度。






